Solving the inverse materials design problem with alchemical chirality
by Carey Sargent, NCCR MARVEL, EPFL
Virtually simulating molecules and materials to predict their physical, material and chemical properties has become a routine, if computationally demanding, tool in the molecular and materials sciences. The hope is that computational materials and molecular design could one day lead to automatized experimental design and discovery.
Increasingly rapid progress in the development of computer hardware and artificial intelligence has led to initial examples of integrating software and robotics to perform experimental sequences, establish rules and trends among properties and materials and even to synthesize them. The goal of materials on demand remains elusive though, even simply in terms of simulation.
Continuing the tradition of using empirical trends to guide experimental design with modern systematic attempts to establish and apply rules in terms of quantitative structure-property relationships have led to computationally advanced bio-, chem-, and materials-informatics techniques. The methods developed tend to be intrinsically limited to certain domains of application though and do not scale because of their empirical nature. Thoroughly exploring the chemical compound space, that is, all conceivable molecules or materials—a number that scales combinatorially—requires that the quantum mechanics of electrons be taken into account. This helps explain why ab initio-based materials design approaches such as density functional theory have led the way for more than 20 years and have played a significant role in popularizing the use of accurate, efficient quantum methods.
Sampling the chemical compound space somewhat randomly, even when using efficient optimization algorithms, is a huge undertaking and doesn’t take the many underlying relations between properties and materials into account. Quantum machine learning models are able to exploit these correlations hidden in the data statistically and have accelerated exploration. The efficiency and transferability of ML benefits greatly from the explicit enforcement of known relationships directly in the construction of the model construction—specific examples include explicitly imposing forces and curvatures in the loss function, spatial symmetry relations, or even arbitrary differential relations. That said, acquiring training data in sufficient quantity and quality remains a huge effort, even for the most efficient and transferable statistical models.
In the paper Simplifying inverse material design problems for fixed lattices with alchemical chirality, Anatole von Lilienfeld, professor at the University of Basel and at the University of Vienna and Guido Falk von Rudorff, a postdoc in the same group, introduced the idea of a new symmetry relation that will allow researchers to simplify the the so-called inverse materials design problem. While researchers have gotten quite good at predicting, for example, the electronic properties of a material given its molecular structure using first principles calculations and ML, searching for the right material for a given application requires working backwards—we know the desired properties but have to find the materials that feature them. The new fundamental notion, consistent with the ab initio view of matter, will allow researchers to solve this problem non-empirically and more efficiently, the researchers said.
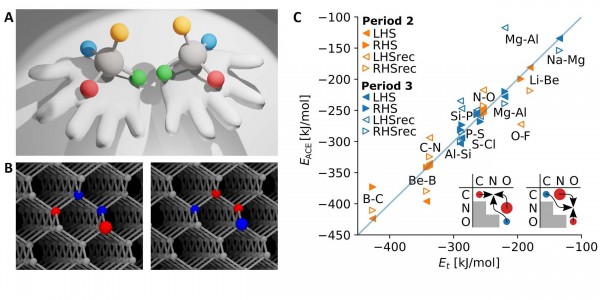
Figure 1
Considerations of spatial symmetry have played a significant role in unravelling some of the fundamental laws of nature and are used in many fields. In ab initio calculations, arguments based on symmetry group theory are often used to reduce computational complexity and load. Having symmetry constraints on compositional degrees of freedom would be very helpful in establishing general rules among distinct materials and properties. This would also improve our understanding of chemical compound space. The authors have therefore proposed a concept they call alchemical chirality—a reflection plane in the nuclear charges at fixed atomic positions as entered into the electronic Schroedinger equation.
An example is given in Figure 1, which shows alchemical chirality at four sites in a diamond cubic lattice, relating boron-doped alchemical enantiomers through alchemical reflection (boron, nitrogen, and carbon are shown in red, blue, and gray, respectively). The shift of the dopant atom sequence from NBBN to BNNB is effectively an alchemical reflection of corresponding nuclear charge differences around a perfectly symmetric nuclear charge reference plane spanned by the carbon atoms in pristine diamond. No other spatial symmetry operation, that is, no rotation, reflection or inversion, can interconvert these constitutional isomers—the concept of 4-dimensional chemical chirality is then necessary. It should be noted too that chirality crucially depends on dimensionality. As an example, they give the letter L, which is chiral within two dimensions.
Though restricting the alchemical chirality to fixed atomic positions might seem severe, fixed configurational framework classes are very important and relevant to materials design applications. Specifically, the authors discuss the implications of alchemical chirality for system classes that are low dimensional in terms of structural degrees of freedom and where the problem is dominated by the combinatorial scaling linked to varying chemical composition. There are many such examples, including the graphitic materials widely used in nano-technological applications, in inorganic materials such as MAX-phases, or in organic electronics, e.g. polycyclic aromatic hydrocarbon derivatives, as well as other rigid scaffolds, such as Metal-Organic-Frameworks or perovskites. All of these materials, the authors say, could all be directly amenable to alchemical chirality estimates (ACE).
For all of these classes, the number of possible materials increases combinatorially with the number of building blocks. For real-world applications, quantum chemistry models often need to include defects, and this makes the chemical space under consideration even larger. For particularly rigid frameworks and extended periodic materials, only local and low-dimensional geometric responses to change of composition are typically observed. As such, ACE amount to an additional, complementary way of rigorously sampling compositional ensembles within a given framework class. In the paper, the researchers demonstrate the use of ACE as an enabling tool for the systematic identification of structure property relations by identifying design rules from an analysis of more than 400 million alchemical estimates of BN-doped derivatives in the picene framework.
References:
G. von Rudorff and O. A. von Lilienfeld, Solving the inverse materials design problem with alchemical chirality, to be published in Science Advances, arXiv:2008.02784 (2020). [Open Access URL]
Low-volume newsletters, targeted to the scientific and industrial communities.
Subscribe to our newsletter