New approach for a unified formalism for spectral and thermodynamic properties of interacting-electron systems
by Carey Sargent, EPFL, NCCR MARVEL
A need for better comparisons between computational predictions and experimental results and increased trust in the calculations behind materials design is fuelling demand for ever more accurate predictions of materials spectra and thermodynamics.
While the widely used and successful density-functional theory (DFT)—a quantum mechanical modelling method allowing for the investigation of the electronic structure of many-body systems in a computationally simplified manner—allows for the accurate calculation of ground-state quantities for most materials, it often reaches its limits with the computation of spectral and thermodynamic properties for complex materials or strongly-correlated systems.
Approaches that include dynamical potentials such as many-body perturbation theory or dynamical mean-field theory have, in principle, the flexibility to overcome the limitations of DFT and allow for better predictions. In such so-called embedding methods, which formulate simple models, molecules or materials in terms of a single particle coupled to an effective environment, static potentials become dynamical or self-energy operators. Frequency acts as the embedding parameter, allowing for energy or particle exchange between the system and its environment.
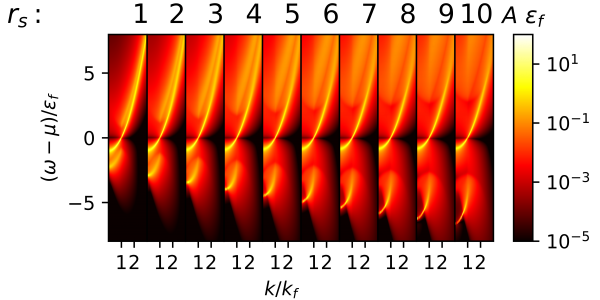
Figure 1. Spectral function of the Homogeneous Electron Gas at several densities (rs) as function of momentum and energy in units of the Fermi momentum and Fermi energy, respectively. With the use of algorithmic inversion method, the sum-over-pole form for such functions is known, allowing for an accurate computation of the thermodynamics, e.g., the total energy, of the system.
Determining the dynamical potential ultimately allows, through a series of calculations, for the computation of the spectral function. This is closely related to angle-resolved photoemission spectroscopy, and thus it contains the information on the excitations of the material’s particles. The frequency integration of these quantities also provides information on the thermodynamics of the system studied, e.g., the number of particles or the total energy. Though powerful, such an approach is limited by the difficulty of computing accurate integrals of propagators over frequencies, which have intrinsically non-smooth natures.
Though this problem can be addressed using an imaginary-frequency-axes formalism based on the computation of integrals from a smoother region, doing this limits the accuracy of the spectral predictions. A formalism that can accurately address both the spectra and thermodynamic properties of a material is therefore greatly needed. In the paper “Unified Green's function approach for spectral and thermodynamic properties from algorithmic inversion of dynamical potentials,” recently published in Physical Review Research, authors Tommaso Chiarotti and Nicola Marzari of NCCR MARVEL and the Theory and Simulations of Materials lab at EPFL and colleague Andrea Ferretti of Centro S3, CNR–Istituto Nanoscienze, present just such an approach. Dubbed the algorithmic inversion method, applied on sum-over-pole representations (AIM-SOP), the novel technique addresses the simultaneous calculation of accurate spectral and thermodynamic quantities.
Starting from a mathematical approach to propagators—a term referring to a function specifying the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum—that do not interact, the researchers go on to develop a sum-over-poles (SOP) representation that is flexible enough to include interacting-particle effects. An essential step of the process involved developing an improved set of basis functions that allow for fast-decaying-represented spectral functions.
Then, they show that a dynamical potential expanded as sum over poles allows for the so-called algorithmic inversion method. This approach, based on a mapping to a matrix diagonalization and knowledge of the non-interacting propagator and the SOP of the self-energy, is the exact generalization of a (static) Hamiltonian diagonalization to an embedded system, and allows for an exact solution of the fundamental equation for such problems, the Dyson equation. The solution yields the Green's function for the system yielding both the spectra and the thermodynamics.
To test the accuracy and efficiency of their unified approach, the researchers applied the developed AIM-SOP method to the homogeneous electron gas, a model of electrons that interact in a solid where the positive charges are assumed to be uniformly distributed in space. The method provides accurate spectra simultaneously with precise frequency-integrated quantities, e.g., occupation numbers and total energies. Their results were similar to those produced from earlier studies for the spectral function, also finding quantitative agreement with previous investigations for the total energy of the gas, in which calculations were performed on the imaginary axis.
Reference:
Tommaso Chiarotti, Nicola Marzari, and Andrea Ferretti. Unified Green's function approach for spectral and thermodynamic properties from algorithmic inversion of dynamical potentials. Phys. Rev. Research 4, 013242
Low-volume newsletters, targeted to the scientific and industrial communities.
Subscribe to our newsletter